Contents

Statistics in Python

In this section, we will cover how you can use Python to do some statistics. There are many packages to do so, but we will focus on four:

This notebook is strongly based on the scipy-lectures.org section about statistics.

Data representation and interaction

Data as a table

The setting that we consider for statistical analysis is that of multiple observations or samples described by a set of different attributes or features. The data can than be seen as a 2D table, or matrix, with columns giving the different attributes of the data, and rows the observations. For instance, the data contained in data/brain_size.csv:

!head data/brain_size.csv

"";"Hair";"FSIQ";"VIQ";"PIQ";"Weight";"Height";"MRI_Count"
"1";"light";133;132;124;"118";"64.5";816932
"2";"dark";140;150;124;".";"72.5";1001121
"3";"dark";139;123;150;"143";"73.3";1038437
"4";"dark";133;129;128;"172";"68.8";965353
"5";"light";137;132;134;"147";"65.0";951545
"6";"light";99;90;110;"146";"69.0";928799
"7";"light";138;136;131;"138";"64.5";991305
"8";"light";92;90;98;"175";"66.0";854258
"9";"dark";89;93;84;"134";"66.3";904858

The pandas data-frame

Creating dataframes: reading data files or converting arrays

Reading from a CSV file

Using the above CSV file that gives observations of brain size and weight and IQ (Willerman et al. 1991), the data are a mixture of numerical and categorical values::

import pandas as pd
data = pd.read_csv('data/brain_size.csv', sep=';', na_values=".", index_col=0)
data
Hair FSIQ VIQ PIQ Weight Height MRI_Count
1 light 133 132 124 118.0 64.5 816932
2 dark 140 150 124 NaN 72.5 1001121
3 dark 139 123 150 143.0 73.3 1038437
4 dark 133 129 128 172.0 68.8 965353
5 light 137 132 134 147.0 65.0 951545
6 light 99 90 110 146.0 69.0 928799
7 light 138 136 131 138.0 64.5 991305
8 light 92 90 98 175.0 66.0 854258
9 dark 89 93 84 134.0 66.3 904858
10 dark 133 114 147 172.0 68.8 955466
11 light 132 129 124 118.0 64.5 833868
12 dark 141 150 128 151.0 70.0 1079549
13 dark 135 129 124 155.0 69.0 924059
14 light 140 120 147 155.0 70.5 856472
15 light 96 100 90 146.0 66.0 878897
16 light 83 71 96 135.0 68.0 865363
17 light 132 132 120 127.0 68.5 852244
18 dark 100 96 102 178.0 73.5 945088
19 light 101 112 84 136.0 66.3 808020
20 dark 80 77 86 180.0 70.0 889083
21 dark 83 83 86 NaN NaN 892420
22 dark 97 107 84 186.0 76.5 905940
23 light 135 129 134 122.0 62.0 790619
24 dark 139 145 128 132.0 68.0 955003
25 light 91 86 102 114.0 63.0 831772
26 dark 141 145 131 171.0 72.0 935494
27 light 85 90 84 140.0 68.0 798612
28 dark 103 96 110 187.0 77.0 1062462
29 light 77 83 72 106.0 63.0 793549
30 light 130 126 124 159.0 66.5 866662
31 light 133 126 132 127.0 62.5 857782
32 dark 144 145 137 191.0 67.0 949589
33 dark 103 96 110 192.0 75.5 997925
34 dark 90 96 86 181.0 69.0 879987
35 light 83 90 81 143.0 66.5 834344
36 light 133 129 128 153.0 66.5 948066
37 dark 140 150 124 144.0 70.5 949395
38 light 88 86 94 139.0 64.5 893983
39 dark 81 90 74 148.0 74.0 930016
40 dark 89 91 89 179.0 75.5 935863

Creating from arrays

A pandas.DataFrame can also be seen as a dictionary of 1D ‘series’, eg arrays or lists. If we have 3 numpy arrays:

import numpy as np
t = np.linspace(-6, 6, 20)
sin_t = np.sin(t)
cos_t = np.cos(t)

We can expose them as a pandas.DataFrame:

pd.DataFrame({'t': t, 'sin': sin_t, 'cos': cos_t}).head()
t sin cos
0 -6.000000 0.279415 0.960170
1 -5.368421 0.792419 0.609977
2 -4.736842 0.999701 0.024451
3 -4.105263 0.821291 -0.570509
4 -3.473684 0.326021 -0.945363

Other inputs: pandas can input data from SQL, excel files, or other formats. See the pandas documentation.

Manipulating data

data is a pandas.DataFrame, that resembles R’s dataframe:

data.shape    # 40 rows and 8 columns

(40, 7)

data.columns  # It has columns

Index(['Hair', 'FSIQ', 'VIQ', 'PIQ', 'Weight', 'Height', 'MRI_Count'], dtype='object')

print(data['Hair'].head())  # Columns can be addressed by name

1    light
2     dark
3     dark
4     dark
5    light
Name: Hair, dtype: object

# Simpler selector
data[data['Hair'] == 'light']['VIQ'].mean()

109.45

Note: For a quick view on a large dataframe, use its describe pandas.DataFrame.describe.

data.describe()
FSIQ VIQ PIQ Weight Height MRI_Count
count 40.000000 40.000000 40.00000 38.000000 39.000000 4.000000e+01
mean 113.450000 112.350000 111.02500 151.052632 68.525641 9.087550e+05
std 24.082071 23.616107 22.47105 23.478509 3.994649 7.228205e+04
min 77.000000 71.000000 72.00000 106.000000 62.000000 7.906190e+05
25% 89.750000 90.000000 88.25000 135.250000 66.000000 8.559185e+05
50% 116.500000 113.000000 115.00000 146.500000 68.000000 9.053990e+05
75% 135.500000 129.750000 128.00000 172.000000 70.500000 9.500780e+05
max 144.000000 150.000000 150.00000 192.000000 77.000000 1.079549e+06 
# Frequency count for a given column
data['Height'].value_counts()

64.5    4
69.0    3
68.0    3
66.5    3
63.0    2
66.0    2
70.0    2
70.5    2
68.8    2
66.3    2
75.5    2
72.0    1
77.0    1
76.5    1
73.5    1
68.5    1
62.5    1
67.0    1
74.0    1
73.3    1
65.0    1
72.5    1
62.0    1
Name: Height, dtype: int64

# Dummy-code # of hair color (i.e., get N-binary columns)
pd.get_dummies(data['Hair'])[:15]
dark light
1 0 1
2 1 0
3 1 0
4 1 0
5 0 1
6 0 1
7 0 1
8 0 1
9 1 0
10 1 0
11 0 1
12 1 0
13 1 0
14 0 1
15 0 1

The split-apply-combine pattern

  • A very common data processing strategy is to…

    • Split the dataset into groups

    • Apply some operation(s) to each group

    • (Optionally) combine back into one dataset

Pandas provides powerful and fast tools for this. For example the groupby function.

groupby: splitting a dataframe on values of categorical variables:

groupby_hair = data.groupby('Hair')
for hair, value in groupby_hair['VIQ']:
     print((hair, value.mean()))

('dark', 115.25)
('light', 109.45)

groupby_hair is a powerful object that exposes many operations on the resulting group of dataframes:

groupby_hair.mean()
FSIQ VIQ PIQ Weight Height MRI_Count
Hair
dark 115.0 115.25 111.60 166.444444 71.431579 954855.4
light 111.9 109.45 110.45 137.200000 65.765000 862654.6

Plotting data

Pandas comes with some plotting tools (pandas.tools.plotting, using matplotlib behind the scene) to display statistics of the data in dataframes.

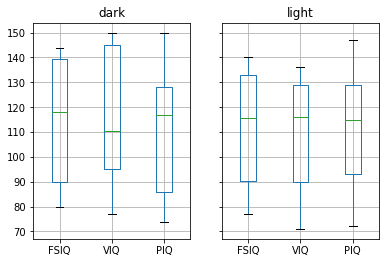
For example, let’s use boxplot (in this case even groupby_hair.boxplot) to better understand the structure of the data.

%matplotlib inline
groupby_hair.boxplot(column=['FSIQ', 'VIQ', 'PIQ']);
_images/intro_statistics_26_0.png

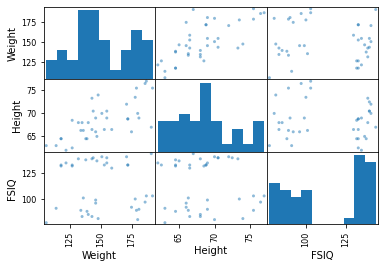
Scatter matrices

pd.plotting.scatter_matrix(data[['Weight', 'Height', 'FSIQ']]);
_images/intro_statistics_28_0.png

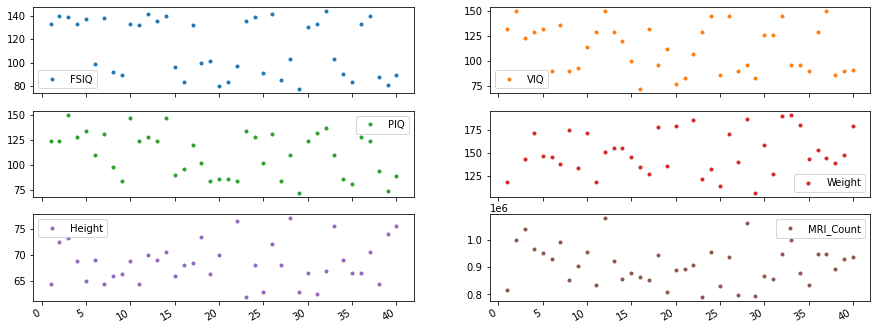
Plot content of a dataset

data.head()
Hair FSIQ VIQ PIQ Weight Height MRI_Count
1 light 133 132 124 118.0 64.5 816932
2 dark 140 150 124 NaN 72.5 1001121
3 dark 139 123 150 143.0 73.3 1038437
4 dark 133 129 128 172.0 68.8 965353
5 light 137 132 134 147.0 65.0 951545 
data.plot(lw=0, marker='.', subplots=True, layout=(-1, 2), figsize=(15, 6));
_images/intro_statistics_31_0.png

Pingouin is an open-source statistical package written in Python 3 and based mostly on Pandas and NumPy.

  • ANOVAs: one- and two-ways, repeated measures, mixed, ancova

  • Post-hocs tests and pairwise comparisons

  • Robust correlations

  • Partial correlation, repeated measures correlation and intraclass correlation

  • Linear/logistic regression and mediation analysis

  • Bayesian T-test and Pearson correlation

  • Tests for sphericity, normality and homoscedasticity

  • Effect sizes and power analysis

  • Parametric/bootstrapped confidence intervals around an effect size or a correlation coefficient

  • Circular statistics

  • Plotting: Bland-Altman plot, Q-Q plot, etc…

Pingouin is designed for users who want simple yet exhaustive statistical functions.

**material scavenged from 10 minutes to Pingouin and the pingouin docs

import pingouin as pg

Measures of correlation

“In the broadest sense correlation is any statistical association, though in common usage it most often refers to how close two variables are to having a linear relationship with each other” - Wikipedia

When talking about correlation, we commonly mean the Pearson correlation coefficient, also referred to as Pearson’s r

pearson_correlation = pg.corr(data['FSIQ'], data['VIQ'])
display(pearson_correlation)
cor_coeeficient = pearson_correlation['r']
n =  len(data) # sample size
n r CI95% r2 adj_r2 p-val BF10 power
pearson 40 0.947 [0.9, 0.97] 0.896 0.891 2.789130e-20 2.120526e+17 1.0

Test summary

  • ‘n’ : Sample size (after NaN removal)

  • ‘outliers’ : number of outliers (only for ‘shepherd’ or ‘skipped’)

  • ‘r’ : Correlation coefficient

  • ‘CI95’ : 95% parametric confidence intervals

  • ‘r2’ : R-squared

  • ‘adj_r2’ : Adjusted R-squared

  • ‘p-val’ : one or two tailed p-value

  • ‘BF10’ : Bayes Factor of the alternative hypothesis (Pearson only)

  • ‘power’ : achieved power of the test (= 1 - type II error)

Before we calculate: Testing statistical premises

Statistical procedures can be classfied into either parametric or non parametric prcedures, which require different necessary preconditions to be met in order to show consistent/robust results. Generally people assume that their data follows a gaussian distribution, which allows for parametric tests to be run. Nevertheless it is essential to first test the distribution of your data to decide if the assumption of normally distributed data holds, if this is not the case we would have to switch to non parametric tests.

Shapiro Wilk normality test

Standard procedure to test for normal distribution. Tests if the distribution of you data deviates significtanly from a normal distribution. returns:

  • normal : boolean True if x comes from a normal distribution.

  • p : float P-value.

# Return a boolean (true if normal) and the associated p-value
normal, p = pg.normality(data['Height'], data['VIQ'], alpha=.05)
print(normal, p)

[ True False] [1.    0.008]

Henze-Zirkler multivariate normality test

Same procedure for multivariate normal distributions

returns

  • normal : boolean True if X comes from a multivariate normal distribution.

  • p : float P-value.

# Return a boolean (true if normal) and the associated p-value
np.random.seed(123)
mean, cov, n = [4, 6], [[1, .5], [.5, 1]], 30
X = np.random.multivariate_normal(mean, cov, n)
normal, p = pg.multivariate_normality(X, alpha=.05)
print(normal, p)

True 0.7523511059223016

Mauchly test for sphericity

“Sphericity is the condition where the variances of the differences between all combinations of related groups (levels) are equal. Violation of sphericity is when the variances of the differences between all combinations of related groups are not equal.” - https://statistics.laerd.com/statistical-guides/sphericity-statistical-guide.php

returns

  • spher : boolean True if data have the sphericity property.

  • W : float Test statistic

  • chi_sq : float Chi-square statistic

  • ddof : int Degrees of freedom

  • p : float P-value.

pg.sphericity(data)

(False, 0.0, 3069.927, 20, 0.0)

Testing for homoscedasticity

“In statistics, a sequence or a vector of random variables is homoscedastic /ˌhoʊmoʊskəˈdæstɪk/ if all random variables in the sequence or vector have the same finite variance.” - wikipedia

returns:

  • equal_var : boolean True if data have equal variance.

  • p : float P-value.

Note: This function first tests if the data are normally distributed using the Shapiro-Wilk test. If yes, then the homogeneity of variances is measured using the Bartlett test. If the data are not normally distributed, the Levene test, which is less sensitive to departure from normality, is used.

np.random.seed(123)
# Scale = standard deviation of the distribution.
array_1 = np.random.normal(loc=0, scale=1., size=100)
array_2 = np.random.normal(loc=0, scale=0.8,size=100)
print(np.var(array_1), np.var(array_2))

equal_var, p = pg.homoscedasticity(array_1, array_2, alpha=.05)
print(equal_var, p)

1.2729265592243306 0.6022425373276372
False 0.0

Parametric tests

Student’s t-test: the simplest statistical test

1-sample t-test: testing the value of a population mean

tests if the population mean of data is likely to be equal to a given value (technically if observations are drawn from a Gaussian distributions of given population mean).

pingouin.ttest returns the T_statistic, the p-value, the [degrees of freedom](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics), the Cohen d effect size, the achieved [power](https://en.wikipedia.org/wiki/Power_(statistics)) of the test ( = 1 - type II error (beta) = P(Reject H0|H1 is true)), and the Bayes Factor of the alternative hypothesis

pg.ttest(data['VIQ'],0)
T p-val dof tail cohen-d power BF10
T-test 30.088 1.328920e-28 39 two-sided 4.757 1.0 1.900865e+25

2-sample t-test: testing for difference across populations

We have seen above that the mean VIQ in the black hair and white hair populations were different. To test if this is significant, we do a 2-sample t-test:

light_viq = data[data['Hair'] == 'light']['VIQ']
dark_viq = data[data['Hair'] == 'dark']['VIQ']

pg.ttest(light_viq, dark_viq)
T p-val dof tail cohen-d power BF10
T-test -0.773 0.444529 38 two-sided 0.244 0.114 0.391

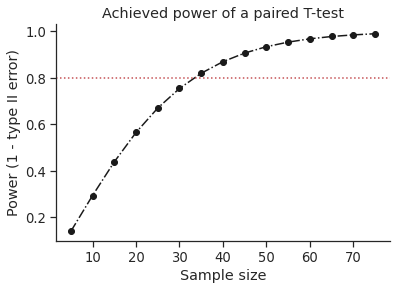
Plot achieved power of a paired T-test

Plot the curve of achieved power given the effect size (Cohen d) and the sample size of a paired T-test.

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='ticks', context='notebook', font_scale=1.2)

d = 0.5  # Fixed effect size
n = np.arange(5, 80, 5)  # Incrementing sample size

# Compute the achieved power
pwr = pg.power_ttest(d=d, n=n, contrast='paired', tail='two-sided')

# Start the plot
plt.plot(n, pwr, 'ko-.')
plt.axhline(0.8, color='r', ls=':')
plt.xlabel('Sample size')
plt.ylabel('Power (1 - type II error)')
plt.title('Achieved power of a paired T-test')
sns.despine()
_images/intro_statistics_56_0.png

Non parametric tests:

Unlike the parametric test these do not require the assumption of normal distributions.

“Mann-Whitney U Test (= Wilcoxon rank-sum test). It is the non-parametric version of the independent T-test. Mwu tests the hypothesis that data in x and y are samples from continuous distributions with equal medians. The test assumes that x and y are independent. This test corrects for ties and by default uses a continuity correction.” - mwu-function

Test summary

  • ‘W-val’ : W-value

  • ‘p-val’ : p-value

  • ‘RBC’ : matched pairs rank-biserial correlation (effect size)

  • ‘CLES’ : common language effect size

pg.mwu(light_viq, dark_viq)
U-val p-val RBC CLES
MWU 164.5 0.342289 0.1775 0.575

“Wilcoxon signed-rank test is the non-parametric version of the paired T-test.

The Wilcoxon signed-rank test tests the null hypothesis that two related paired samples come from the same distribution. A continuity correction is applied by default.” - wilcoxon - func

# example from the function definition
# Wilcoxon test on two related samples.
x = [20, 22, 19, 20, 22, 18, 24, 20]
y = [38, 37, 33, 29, 14, 12, 20, 22]
print("Medians = %.2f - %.2f" % (np.median(x), np.median(y)))
pg.wilcoxon(x, y, tail='two-sided')

Medians = 20.00 - 25.50

/opt/miniconda-latest/envs/neuro/lib/python3.7/site-packages/scipy/stats/morestats.py:2879: UserWarning: Sample size too small for normal approximation.
  warnings.warn("Sample size too small for normal approximation.")
W-val p-val RBC CLES
Wilcoxon 9.0 0.043089 0.5 0.609375

scipy.stats - Hypothesis testing: comparing two groups

For simple statistical tests, it is also possible to use the scipy.stats sub-module of scipy.

from scipy import stats

1-sample t-test: testing the value of a population mean

scipy.stats.ttest_1samp tests if the population mean of data is likely to be equal to a given value (technically if observations are drawn from a Gaussian distributions of given population mean). It returns the T statistic, and the p-value (see the function’s help):

stats.ttest_1samp(data['VIQ'], 100)

Ttest_1sampResult(statistic=3.3074146385401786, pvalue=0.002030117404781822)

With a p-value of 10^-28 we can claim that the population mean for the IQ (VIQ measure) is not 0.

2-sample t-test: testing for difference across populations

We have seen above that the mean VIQ in the dark hair and light hair populations were different. To test if this is significant, we do a 2-sample t-test with scipy.stats.ttest_ind:

light_viq = data[data['Hair'] == 'light']['VIQ']
dark_viq = data[data['Hair'] == 'dark']['VIQ']
stats.ttest_ind(light_viq, dark_viq)

Ttest_indResult(statistic=-0.7726161723275011, pvalue=0.44452876778583217)

Paired tests: repeated measurements on the same indivuals

PIQ, VIQ, and FSIQ give 3 measures of IQ. Let us test if FISQ and PIQ are significantly different. We can use a 2 sample test:

stats.ttest_ind(data['FSIQ'], data['PIQ'])

Ttest_indResult(statistic=0.465637596380964, pvalue=0.6427725009414841)

The problem with this approach is that it forgets that there are links between observations: FSIQ and PIQ are measured on the same individuals.

Thus the variance due to inter-subject variability is confounding, and can be removed, using a “paired test”, or “repeated measures test”:

stats.ttest_rel(data['FSIQ'], data['PIQ'])

Ttest_relResult(statistic=1.7842019405859857, pvalue=0.08217263818364236)

This is equivalent to a 1-sample test on the difference::

stats.ttest_1samp(data['FSIQ'] - data['PIQ'], 0)

Ttest_1sampResult(statistic=1.7842019405859857, pvalue=0.08217263818364236)

T-tests assume Gaussian errors. We can use a Wilcoxon signed-rank test, that relaxes this assumption:

stats.wilcoxon(data['FSIQ'], data['PIQ'])

WilcoxonResult(statistic=274.5, pvalue=0.10659492713506856)

Note: The corresponding test in the non paired case is the Mann–Whitney U test, scipy.stats.mannwhitneyu.

statsmodels - use “formulas” to specify statistical models in Python

Use statsmodels to perform linear models, multiple factors or analysis of variance.

A simple linear regression

Given two set of observations, x and y, we want to test the hypothesis that y is a linear function of x.

In other terms:

\(y = x * coef + intercept + e\)

where \(e\) is observation noise. We will use the statsmodels module to:

  1. Fit a linear model. We will use the simplest strategy, ordinary least squares (OLS).

  2. Test that \(coef\) is non zero.

First, we generate simulated data according to the model:

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-5, 5, 20)
np.random.seed(1)

# normal distributed noise
y = -5 + 3*x + 4 * np.random.normal(size=x.shape)

# Create a data frame containing all the relevant variables
data = pd.DataFrame({'x': x, 'y': y})

plt.plot(x, y, 'o');
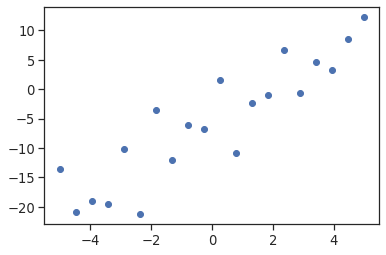
_images/intro_statistics_81_0.png

Then we specify an OLS model and fit it:

from statsmodels.formula.api import ols
model = ols("y ~ x", data).fit()

Note: For more about “formulas” for statistics in Python, see the statsmodels documentation.

We can inspect the various statistics derived from the fit::

print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.804
Model:                            OLS   Adj. R-squared:                  0.794
Method:                 Least Squares   F-statistic:                     74.03
Date:                Sat, 07 Nov 2020   Prob (F-statistic):           8.56e-08
Time:                        20:11:18   Log-Likelihood:                -57.988
No. Observations:                  20   AIC:                             120.0
Df Residuals:                      18   BIC:                             122.0
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -5.5335      1.036     -5.342      0.000      -7.710      -3.357
x              2.9369      0.341      8.604      0.000       2.220       3.654
==============================================================================
Omnibus:                        0.100   Durbin-Watson:                   2.956
Prob(Omnibus):                  0.951   Jarque-Bera (JB):                0.322
Skew:                          -0.058   Prob(JB):                        0.851
Kurtosis:                       2.390   Cond. No.                         3.03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Terminology

Statsmodels uses a statistical terminology: the y variable in statsmodels is called endogenous while the x variable is called exogenous. This is discussed in more detail here. To simplify, y (endogenous) is the value you are trying to predict, while x (exogenous) represents the features you are using to make the prediction.

Categorical variables: comparing groups or multiple categories

Let us go back the data on brain size:

data = pd.read_csv('data/brain_size.csv', sep=';', na_values=".")

We can write a comparison between IQ of people with dark and light hair using a linear model:

model = ols("VIQ ~ Hair + 1", data).fit()
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    VIQ   R-squared:                       0.015
Model:                            OLS   Adj. R-squared:                 -0.010
Method:                 Least Squares   F-statistic:                    0.5969
Date:                Sat, 07 Nov 2020   Prob (F-statistic):              0.445
Time:                        20:11:18   Log-Likelihood:                -182.42
No. Observations:                  40   AIC:                             368.8
Df Residuals:                      38   BIC:                             372.2
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
=================================================================================
                    coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------
Intercept       115.2500      5.308     21.712      0.000     104.504     125.996
Hair[T.light]    -5.8000      7.507     -0.773      0.445     -20.997       9.397
==============================================================================
Omnibus:                       26.188   Durbin-Watson:                   1.709
Prob(Omnibus):                  0.000   Jarque-Bera (JB):                3.703
Skew:                           0.010   Prob(JB):                        0.157
Kurtosis:                       1.510   Cond. No.                         2.62
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Tips on specifying model

Forcing categorical - the ‘Hair’ is automatically detected as a categorical variable, and thus each of its different values is treated as different entities.

An integer column can be forced to be treated as categorical using:

model = ols('VIQ ~ C(Hair)', data).fit()

Intercept: We can remove the intercept using - 1 in the formula, or force the use of an intercept using + 1.

Multiple Regression: including multiple factors

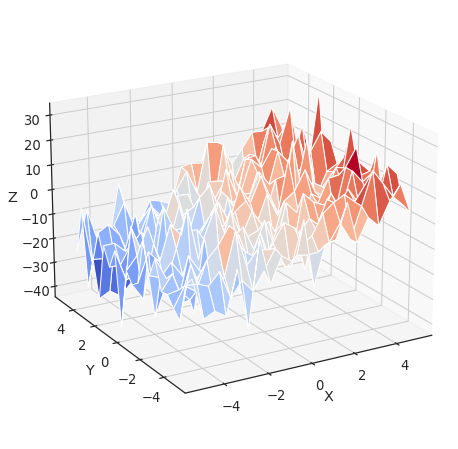
Consider a linear model explaining a variable z (the dependent variable) with 2 variables x and y:

\(z = x \, c_1 + y \, c_2 + i + e\)

Such a model can be seen in 3D as fitting a plane to a cloud of (x, y, z) points (see the following figure).

from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(-5, 5, 21)

# We generate a 2D grid
X, Y = np.meshgrid(x, x)

# To get reproducable values, provide a seed value
np.random.seed(1)

# Z is the elevation of this 2D grid
Z = -5 + 3*X - 0.5*Y + 8 * np.random.normal(size=X.shape)

# Plot the data
fig = plt.figure(figsize=(8, 8))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, cmap=plt.cm.coolwarm,
                       rstride=1, cstride=1)
ax.view_init(20, -120)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

Text(0.5, 0, 'Z')
_images/intro_statistics_99_1.png

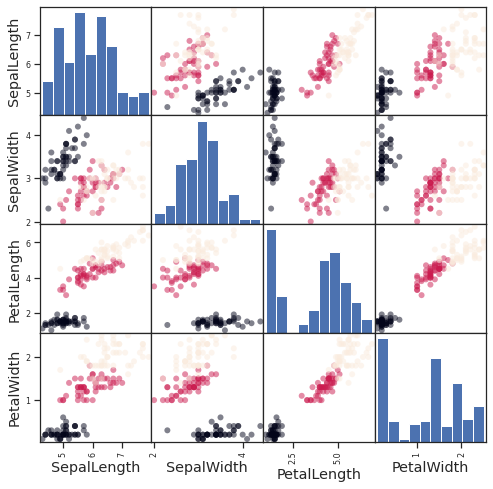
Example: the iris data (data/iris.csv)

Sepal and petal size tend to be related: bigger flowers are bigger! But is there, in addition, a systematic effect of species?

from pandas.plotting import scatter_matrix

#Load the data
data = pd.read_csv('data/iris.csv')

# Express the names as categories
categories = pd.Categorical(data['Species'])

# The parameter 'c' is passed to plt.scatter and will control the color
scatter_matrix(data, c=categories.codes, marker='o', figsize=(8, 8))

# Plot figure
fig.suptitle("blue: setosa, green: versicolor, red: virginica", size=13)
plt.show()
_images/intro_statistics_101_0.png 
data = pd.read_csv('data/iris.csv')
model = ols('SepalWidth ~ Species + PetalLength', data).fit()
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:             SepalWidth   R-squared:                       0.478
Model:                            OLS   Adj. R-squared:                  0.468
Method:                 Least Squares   F-statistic:                     44.63
Date:                Sat, 07 Nov 2020   Prob (F-statistic):           1.58e-20
Time:                        20:11:20   Log-Likelihood:                -38.185
No. Observations:                 150   AIC:                             84.37
Df Residuals:                     146   BIC:                             96.41
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
=========================================================================================
                            coef    std err          t      P>|t|      [0.025      0.975]
-----------------------------------------------------------------------------------------
Intercept                 2.9813      0.099     29.989      0.000       2.785       3.178
Species[T.versicolor]    -1.4821      0.181     -8.190      0.000      -1.840      -1.124
Species[T.virginica]     -1.6635      0.256     -6.502      0.000      -2.169      -1.158
PetalLength               0.2983      0.061      4.920      0.000       0.178       0.418
==============================================================================
Omnibus:                        2.868   Durbin-Watson:                   1.753
Prob(Omnibus):                  0.238   Jarque-Bera (JB):                2.885
Skew:                          -0.082   Prob(JB):                        0.236
Kurtosis:                       3.659   Cond. No.                         54.0
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Post-hoc hypothesis testing: analysis of variance (ANOVA)

In the above iris example, we wish to test if the petal length is different between versicolor and virginica, after removing the effect of sepal width. This can be formulated as testing the difference between the coefficient associated to versicolor and virginica in the linear model estimated above (it is an Analysis of Variance, ANOVA. For this, we write a vector of ‘contrast’ on the parameters estimated: we want to test "name[T.versicolor] - name[T.virginica]", with an F-test:

print(model.f_test([0, 1, -1, 0]))

<F test: F=array([[3.24533535]]), p=0.07369058781700577, df_denom=146, df_num=1>

Is this difference significant?

seaborn - use visualization for statistical exploration

Seaborn combines simple statistical fits with plotting on pandas dataframes.

Let us consider a data giving wages and many other personal information on 500 individuals (Berndt, ER. The Practice of Econometrics. 1991. NY:Addison-Wesley).

import pandas as pd
data = pd.read_csv('data/wages.csv', sep=',')
data.head()
EDUCATION SOUTH HAIR EXPERIENCE UNION WAGE AGE OCCUPATION SECTOR MARR
0 8 0 1 21 0 5.10 35 2 6 1
1 9 0 1 42 0 4.95 57 3 6 1
2 12 0 0 1 0 6.67 19 3 6 1
3 12 0 0 4 0 4.00 22 3 6 0
4 12 0 0 17 0 7.50 35 3 6 0

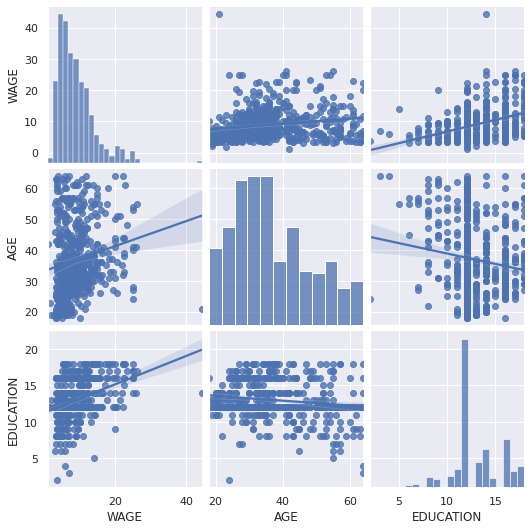
Pairplot: scatter matrices

We can easily have an intuition on the interactions between continuous variables using seaborn.pairplot to display a scatter matrix:

import seaborn
seaborn.set()
seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'], kind='reg')

<seaborn.axisgrid.PairGrid at 0x7fbc60319f90>
_images/intro_statistics_109_1.png

Categorical variables can be plotted as the hue:

seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'], kind='reg', hue='HAIR')

<seaborn.axisgrid.PairGrid at 0x7fbc5b6a3110>
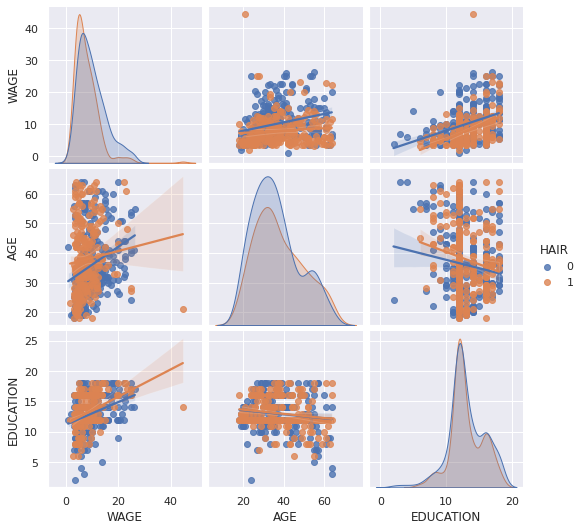
_images/intro_statistics_111_1.png

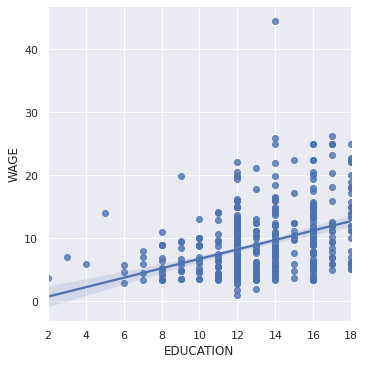
lmplot: plotting a univariate regression

A regression capturing the relation between one variable and another, e.g. wage and eduction, can be plotted using seaborn.lmplot:

seaborn.lmplot(y='WAGE', x='EDUCATION', data=data)

<seaborn.axisgrid.FacetGrid at 0x7fbc5b3c2090>
_images/intro_statistics_113_1.png

Robust regression

Given that, in the above plot, there seems to be a couple of data points that are outside of the main cloud to the right, they might be outliers, not representative of the population, but driving the regression.

To compute a regression that is less sensitive to outliers, one must use a robust model. This is done in seaborn using robust=True in the plotting functions, or in statsmodels by replacing the use of the OLS by a “Robust Linear Model”, statsmodels.formula.api.rlm.

Testing for interactions

Do wages increase more with education for people with dark hair than with light hair?

seaborn.lmplot(y='WAGE', x='EDUCATION', hue='HAIR', data=data)

<seaborn.axisgrid.FacetGrid at 0x7fbc6037d250>
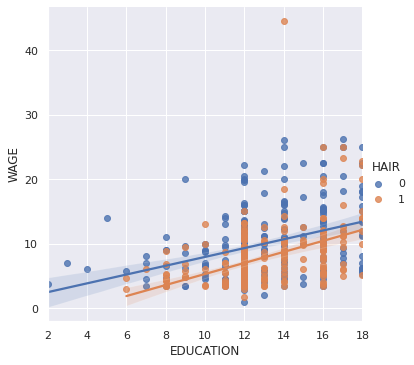
_images/intro_statistics_116_1.png

The plot above is made of two different fits. We need to formulate a single model that tests for a variance of slope across the population. This is done via an “interaction”.

from statsmodels.formula.api import ols
result = ols(formula='WAGE ~ EDUCATION + HAIR + EDUCATION * HAIR', data=data).fit()
print(result.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   WAGE   R-squared:                       0.190
Model:                            OLS   Adj. R-squared:                  0.186
Method:                 Least Squares   F-statistic:                     41.50
Date:                Sat, 07 Nov 2020   Prob (F-statistic):           4.24e-24
Time:                        20:11:33   Log-Likelihood:                -1575.0
No. Observations:                 534   AIC:                             3158.
Df Residuals:                     530   BIC:                             3175.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==================================================================================
                     coef    std err          t      P>|t|      [0.025      0.975]
----------------------------------------------------------------------------------
Intercept          1.1046      1.314      0.841      0.401      -1.476       3.685
EDUCATION          0.6831      0.099      6.918      0.000       0.489       0.877
HAIR              -4.3704      2.085     -2.096      0.037      -8.466      -0.274
EDUCATION:HAIR     0.1725      0.157      1.098      0.273      -0.136       0.481
==============================================================================
Omnibus:                      208.151   Durbin-Watson:                   1.863
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             1278.081
Skew:                           1.587   Prob(JB):                    2.94e-278
Kurtosis:                       9.883   Cond. No.                         170.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Can we conclude that education benefits people with dark hair more than people with light hair?

Take home messages

  • Hypothesis testing and p-value give you the significance of an effect / difference

  • Formulas (with categorical variables) enable you to express rich links in your data

  • Visualizing your data and simple model fits matters!

  • Conditioning (adding factors that can explain all or part of the variation) is an important modeling aspect that changes the interpretation.